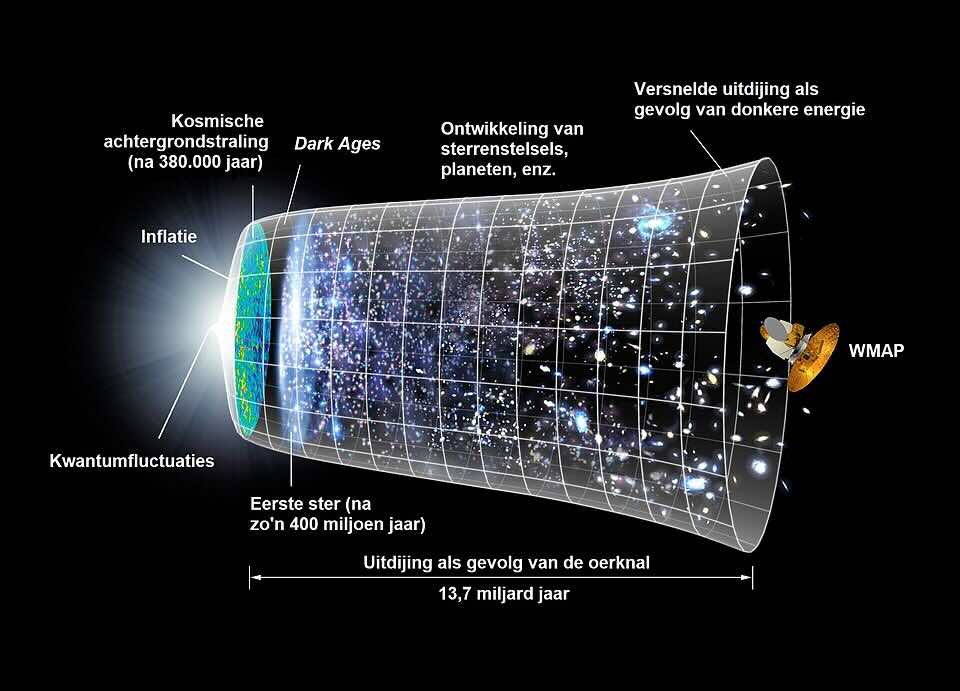
Tijdlijn uitdijing heelal (afb: WikiMedia Commons)
Kosmoloog Eugene Lim van King’s College in Londen en astrofysici Katy Clough van Queen Mary-universiteit in Londen (VK) en Josu Aurrekoetxea van de universiteit van Oxford (VK) zijn de namen van die ‘onverlaten’. Ze stellen ook hun idee voor om een (mogelijk) antwoord te krijgen: het gebruik van complexe rekenmodellen om Einsteins zwaartekrachtvergelijkingen in extreme situaties numeriek (in plaats van exact) op te lossen.
Ze betogen dat numerieke relativiteit steeds vaker in de kosmologie zou moeten worden toegepast om enkele van de grootste vragen van het universum te onderzoeken, waaronder wat er vóór de oerknal gebeurde of dat we in een multiversum leven, of ons universum in botsing is gekomen met een naburige kosmos, of dat ons universum een reeks knallen en kraken heeft doorgemaakt.
Einsteins algemene relativiteitsvergelijkingen beschrijven de zwaartekracht en de beweging van kosmische objecten. Draai de klok ver genoeg terug en je komt doorgaans een singulariteit (eigenaardigheid) tegen, een toestand van oneindige dichtheid en temperatuur waar de natuurwetten instorten.
Kosmologen kunnen Einsteins vergelijkingen in zulke extreme omgevingen simpelweg niet oplossen. Hun normale vereenvoudigingsaannames gaan dan niet meer op. Dezelfde impasse geldt voor objecten met singulariteiten of extreme zwaartekracht, zoals zwarte gaten.
Een probleem zou de kennis kunnen zijn van wat kosmologen als vanzelfsprekend beschouwen. Ze gaan er normaal gesproken van uit dat het universum ‘isotroop en ‘homogeen’ is, dat het er in elke richting hetzelfde uitziet voor elke waarnemer. Dit is een zeer goede benadering voor het universum dat we om ons heen zien en een die het mogelijk maakt om Einsteins vergelijkingen in de meeste kosmische scenario’s gemakkelijk op te lossen, maar is dit een goede benadering voor het universum tijdens de oerknal?
“Je kunt rond de lantaarnpaal zoeken, maar je kunt niet ver voorbij de lantaarnpaal gaan als het donker is. Je kunt die vergelijkingen gewoon niet oplossen,” legt Lim uit. “Numerieke relativiteit stelt je in staat om gebieden buiten de lantaarnpaal te verkennen.”
Voorbij de lantaarnpaal
Numerieke relativiteit werd voor het eerst voorgesteld in de jaren ’60 en ’70 om te proberen te achterhalen welke soorten zwaartekrachtgolven (rimpelingen in de ruimtetijd) zouden worden uitgezonden als zwarte gaten zouden botsen en samensmelten. Dit is een extreem scenario waarbij het onmogelijk is om Einsteins vergelijkingen alleen met pen en papier op te lossen. Dan zijn geavanceerde computeralgoritmes en numerieke benaderingen vereist.
De ontwikkeling ervan kreeg hernieuwde aandacht toen het LIGO-experiment in de jaren ’80 werd voorgesteld, hoewel het probleem pas in 2005 op deze manier werd opgelost. Dat gaf hoop dat de methode ook succesvol kon worden toegepast op andere kosmische puzzels.
Een al lang bestaande puzzel waar Lim bijzonder enthousiast over is, is kosmische inflatie, een periode van extreem snelle expansie in het vroege heelal. Inflatie werd aanvankelijk voorgesteld om te verklaren waarom het heelal eruitziet zoals het er nu uitziet, door een aanvankelijk klein stukje uit te rekken, zodat het heelal er over een enorme afstand hetzelfde uitziet.
Lim: “Als je geen inflatie hebt, vallen veel dingen uit elkaar.” Hoewel inflatie echter helpt om de toestand van het heelal vandaag de dag te verklaren, heeft niemand kunnen verklaren hoe of waarom het heel vroege heelal deze plotselinge, kortstondige groeispurt had.
Het probleem is dat kosmologen, om dit met Einsteins vergelijkingen te onderzoeken, moeten aannemen dat het heelal in de eerste plaats homogeen en isotroop was. Dat zou de inflatie juist moeten verklaren. Als je in plaats daarvan aanneemt dat het in een andere toestand begon, dan heb je volgens Lim niet de symmetrie om je vergelijkingen gemakkelijk op te schrijven.
Numerieke relativiteit zou ons kunnen helpen dit probleem te omzeilen, door radicaal andere beginomstandigheden mogelijk te maken. Het is echter geen eenvoudige puzzel om op te lossen, aangezien er oneindig veel manieren zijn waarop de ruimtetijd er vóór inflatie uit had kunnen zien. Lim hoopt daarom numerieke relativiteit te gebruiken om de voorspellingen te testen die voortkomen uit meer fundamentele theorieën die inflatie genereren, zoals de snaartheorie.
Botsende universums
Er zijn ook andere perspectieven. Natuurkundigen zouden numerieke relativiteit kunnen gebruiken om te proberen te achterhalen wat voor soort zwaartekrachtgolven kunnen worden gegenereerd door hypothetische objecten (kosmische snaren; lange, dunne ‘littekens’ in de ruimtetijd) en zo mogelijk hun bestaan te bevestigen. Ze zouden ook signatuur, ‘blauwe plekken’, aan de hemel kunnen voorspellen als gevolg van botsingen tussen ons universum en naburige universums (als die al bestaan), wat ons zou kunnen helpen de multiversumtheorie te verifiëren.
Spannend genoeg zou numerieke relativiteit ook kunnen helpen onthullen of er vóór de oerknal een universum bestond. Misschien is de kosmos cyclisch en doorloopt die ‘stuiteringen” van oude universums naar nieuwe met herhaalde wedergeboortes, oerknallen en grote klappen. Dat is een zeer moeilijk analytisch probleem.
Lim: “Stuiterende universums zijn een uitstekend voorbeeld, omdat ze een sterke zwaartekracht bereiken waar je niet op je symmetrieën kunt vertrouwen. Verschillende groepen werken er al aan. Vroeger deed niemand dat.”
Variaties zijn zo complex dat de berekeningen supercomputers vereisen. Naarmate de technologie van deze machines verbetert, kunnen we een aanzienlijke verbetering verwachten in ons begrip van het universum. Lim hoopt dat het nieuwe artikel van hem en zijn collega’s de methoden en voordelen van numerieke relativiteit schetst, onderzoekers op verschillende gebieden uiteindelijk op de hoogte kan brengen.
“We hopen die overlap tussen kosmologie en numerieke relativiteit daadwerkelijk te ontwikkelen, zodat numerieke relativisten die geïnteresseerd zijn in het gebruik van hun technieken om kosmologische problemen te onderzoeken, ermee aan de slag kunnen en kosmologen die geïnteresseerd zijn in het oplossen van enkele van de vragen die ze niet kunnen oplossen, numerieke relativiteit kunnen gebruiken.”
Bron: phys.org
